drghirlanda

Here is a bit of combinatorics I encountered when preparing a paper on the co-evolution of behavioral repertoire, brain size, and lifespan (I will talk about the paper another time…). Let’s begin with two definitions:

Definition 1: The falling power 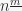is defined as the product 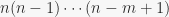, or:

(1)    

If you are familiar with binomial coefficients, they are related to falling powers by .

Definition 2: The Stirling numbers of the second kind are a double series of numbers that tell us how many ways there are to partition objects into non-empty subsets. This is written sometimes and sometimes 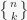. I will use the fancier notation. For example, there are only 3 ways to partition 3 elements in to 2 non-empty subsets: (12)(3), (13)(2), (1)(23), where 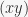means that and have been put together in the same subset. These numbers, beyond the simplest case, are nowhere near intuitive (at least to me). For example, There are 7 ways to partition 4 objects into 2 subsets, hence (you can figure these ways out for yourself), and 1701 ways to partition 8 objects in 4 subsets, hence 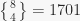 (I suggest you do not try this on your own).

Now, it happens that falling powers and Stirling numbers of the second kind are related by the following identity:

(2)    

I have only seen this equation proved by induction, but working on the above-mentioned paper I stumbled upon a direct proof that goes as follows. Note first that is the number of ways to arrange objects in sequences of length , with repetitions possible (by sequence I mean an ordered selection so that (1,2,2) and (2,1,2) are two different sequences). So we have

(4)    

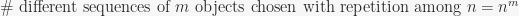
Equation (2) then comes from the fact that its r.h.s. is a different (and more laborious) way to count the same sequences. In other words, we can first count the sequences that we can form using only out of the objects, and then sum over :

(5)    

 Now we have to calculate the expression in the sum. Consider thus constructing a sequence of length out of distinct object, which in turn have been selected among . There are 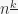ways of selecting which of the objects are going to be part of the sequence, given that the first object out of , the second out of 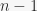, and so on, until the -th object can be selected out of 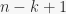. Once we have the objects, in how many ways we can allocate them among the places of the sequence? This is exactly the number of ways in which a set of size can be partitioned in non-empty subsets, or, if you want, the number of ways in which balls can be placed in bins without leaving any one bin empty. Thus

(6)    

which, together with (5), gives (2).